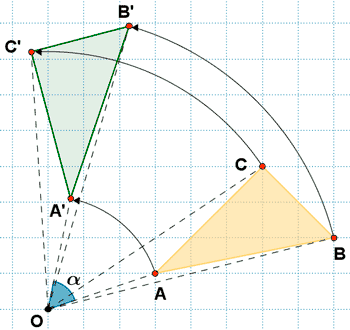
La posición de un punto es rotada alrededor del origen de coordenadas.

El punto P(x, y) está localizado a un ángulo φ del eje x y a una distancia r del origen. Tras rotar el punto a un ángulo θ se obtiene el punto P’(x’, y’).
Así tenemos que:
\begin{equation} \begin{split} x = r\cos(\phi) \\ y = r\sin(\phi) \end{split} \end{equation}
\begin{equation} \begin{split} x' = r\cos(\phi + \theta) \\ y' = r\sin(\phi + \theta) \end{split} \end{equation}
Mediante identidades trigonométricas podemos expandir las ecuaciones para obtener:
\begin{equation} \begin{split} x' = r\cos(\phi)\cos(\theta) - r\sin(\phi)\sin(\theta) \\ y' = r\cos(\phi)\sin(\theta) + r\sin(\phi)\cos(\theta) \end{split} \end{equation}
Y sustituyendo con las definiciones originales de x y y obtenemos:
\begin{equation} \begin{split} x' = x\cos(\theta) - y\sin(\theta) \\ y' = x\sin(\theta) + y\cos(\theta) \end{split} \end{equation}
Sea R(θ) la matriz de rotación sobre el origen, en coordenadas homogéneas la rotación de un punto P alrededor del origen en 2D se puede expresar como el producto matricial de P’ = P × R(θ).
\begin{equation} \begin{bmatrix} x' & y' & 1 \end{bmatrix} = \begin{bmatrix} x & y & 1 \end{bmatrix} \begin{bmatrix} \cos(\theta) & \sin(\theta) & 0 \\ -\sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{equation}